Running Average

• Design Methodologies

The running average filter is a useful way to reduce noise in a system.  One project I recently worked on required a 4 times frequency output from an encoder input.  The problem was the encoder is mounted to the wheel of an old truck and bearing noise was making the original algorithm generate way too many pulses.  The original algorithm worked, but the noise on the input made it useless.

I first implemented the moving average based on this description.  In my notation this is $$M_1=M_0+t_0-A_0$$ where $M_1$ is the next moving average, $M_0$ was the previous moving average, $t_0$ is the measured time between edges and $$A_0=M_0/8$$ is the "oldest" time value.  A flow chart of the algorithm looks like this:

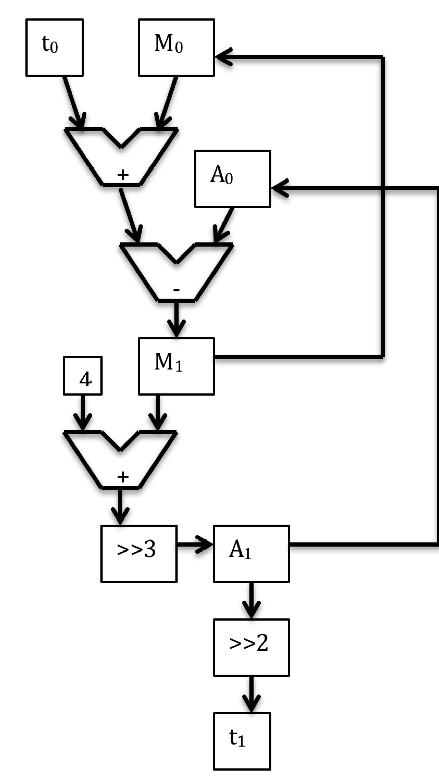
The constant 4 added before the $>>3$ shift is a rounding operation.  This helps smooth out the randomness instead of pure truncation.  Sometimes it's high, sometimes it is low so that on average the time estimate is close to accurate.

Another way to look at this filter is $$M_1 = M_0 + (t_0 - A_0)$$ The running average changes by the difference between the new input and the previous average.  If the difference is small, the average doesn't change.  If the difference is big, it still takes a while to work through the filter before the change is noticed.  This is great for a noisy system because the noise does not pass through to the output.  But long term changes do make it through.  The larger the change, the longer it actually takes.

So in that sense this is not really an accurate moving average.  It does not subtract off the actual data previous to the 8 values which should be summed over.  For some applications this may not be useful, but for the an encoder mounted to a bad wheel bearing it works really well.

Sign in