A Fixed-Point Introduction by Example
Introduction
The finite-word representation of fractional numbers is known as fixed-point. Fixed-point is an interpretation of a 2's compliment number usually signed but not limited to sign representation. It extends our finite-word length from a finite set of integers to a finite set of rational real numbers [1]. A fixed-point representation of a number consists of integer and fractional components. The bit length is defined as:
$$
X_{Nbits} = X_{Integer Nbits} + X_{Fraction Nbits} + 1
$$
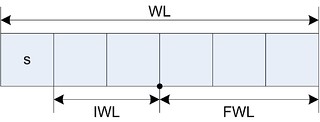
IWL is the integer word length, FWL is the fractional word length, and WL is the word length. For 2's compliment fixed-point representation $ WL = 1 + IWL + FWL $. With this representation the range of the number is $ \left[ -2^{IWL}, 2^{IWL} \right) $ and a step size (resolution) of $ 2^{-FWL} $ [2]. The fixed-point number is defined by its format wl, iwl, fwl or its properties range, resolution, and bias.
As described, a fixed-point number is defined by its range and resolution, instead of the number of bits. When designing a fixed-point system it is logical to use range and resolution requirements and algorithmically resolve the number of bits when it comes time to implement the design. In other words, start with range and resolution when designing / specifying and move to the number of bits required when implementing.
Typically, a short hand is used to represent the format. The Q-format is common when discussing fixed-point processors. I will not use the Q-format because it is not as flexible and can be confusing with the notation used in older fixed-point processor documents [3]. Here I will use an explicit notation, W=(wl,iwl,fwl). This notation defines the number of integer bits, fraction bits, and the total bit length. Example, W=(4,0,3) is a 4-bit number with three fractional bits and a sign bit (the sign bit is implicit). All fixed-point numbers in this post will be 2's complement representation (sign bit is always present).
Why Use Fixed-Point
Why use fixed-point representation? Why not simply normalize all values to an integer range and deal with integers. Depending on your point of view this might be obvious or not. I have found many designers prefer to normalize all values to integers but this produces very unreadable code and documentation. Fixed-point is normally used for convenience (similar to the use of $ \exp{j\omega} $ ). Example, if I am looking at source code and I see:
c0 = fixbv(0.0032, min=-1, max=1, res=2**-15) c1 = fixbv(-0.012, min=-1, max=1, res=2**-15)
I can easily relate this back to the coefficients of a filter but if I see the integer use only:
c0 = intbv(0x0069, min=-2**15, max=2**15) c1 = intbv(-0x0189, min=-2**15, max=2**15)
additional information (documentation) is required. The integer only is difficult to understand what the values are intended to represent. In addition to the representation benefits, tools to handled rounding and overflow are common with fixed-point types.
Now that we have given the basic definition of a fixed-point binary word and given a couple reasons why fixed-point might be used. Let's take a look at some fractional values converted to a fixed-point type. Table 1 is an example of
fixed-point representations.
b7 b6 b5 b4 b3 b2 b1 b0
S F F F F F F F
0 1 0 1 1 0 0 1
+-1 1/2 1/4 1/8 1/16 1/32 1/64 1/128
Value = + 1/2 + 1/8 + 1/16 + 1/128 which equals
= + 0.5 + 0.125 + 0.0625 + 0.0078125
= 0.6953125
The previous two examples illustrate how to represent a fractional value using fixed-point nomenclature. In general the value of the binary word is the following if the integer and fractional parts are treated as separate bit-vectors (i.e. don't share a bit index):
$$
{\displaystyle\sum_{k=0}^{IWL-1} b_{I}[k]2^k} + {\displaystyle\sum_{k=0}^{FWL-1}b_{F}[k]2^{-(k+1)}}
$$
In the above equations, it assumes the bit magnitude increases with the bit index. If visualized the fractional word would be flipped relative to the depiction above.
Multiplication and Addition Examples
The following are fixed-point examples for multiplication and addition. Fixed-point subtraction can be calculated in a similar manner to a 2's complement subtraction (addition with a negative). The difference being the "point" bookkeeping required which is the same as addition. For addition and subtraction the points need to be aligned before the operation (bookkeeping). The "point" bookkeeping is usually calculated at design time and not run time (I say usually because there is the idea of block fixed-point but that is beyond the scope of this post).
Multiplication
Fixed-point multiplication is the same as 2's compliment multiplication but requires the position of the "point" to be determined after the multiplication to interpret the correct result. The determination of the "point's" position is a design task. The actual implementation does not know (or care) where the "point" is located. This is true because the fixed-point multiplication is exactly the same as a 2's complemented multiplication, no special hardware is required.
The following is an example and illustrates $ 6.5625 (W=(8,3,4)) * 4.25 (W=(8,5,2)) $.
0110.1001 == 6.5625
000100.01 == 4.25
01101001
x 00010001
------------
01101001
00000000
00000000
00000000
01101001
00000000
00000000
00000000
--------------------
x000011011111001 == 0000011011.111001 == 27.890625
The number of bits required for the product (result) is the multiplicand's WL + the multiplier's WL ($WL_{multiplicand} + WL_{multiplier}$). It is typical for the results of multiplication (and addition) to be resized and the number of bits reduced. In fixed-point this makes intuitive sense because the smaller fractional bits are discarded and the value is rounded based on the discarded bits. Additional hardware is commonly included to perform the rounding task and reduce the number of bits to a reasonable data-path bus width.
Addition
Addition is a little more complicated because the points need to be aligned before performing the addition. Using the same numbers from the multiplication problem:
0110.1001 == 6.5625
000100.01 == 4.25
0110.1001
+ 000100.01
-------------
001010.1101 == 10.8125
When adding (subtracting) two numbers an additional bit is required for the result. When adding more than two numbers all of the same $WL$ width, the number of bits required for the result is $WL + log_2(N)$ where $N$ is the number of elements being summed.
Conclusion
Fixed-point representation is convienent and useful when dealing with signal processing implementations. This post is a basic introduction to fixed-point numbers. For a more comprehensive coverage of the subject see the references for more information.
[1]: Yates, Randy, "Fixed-Point Arithmetic: An Introduction"
[2]: K.B. Cullen, G.C.M. Silvestre, and .J. Hurley, "Simulation Tools for Fixed Point DSP Algorithms and Architectures"
[3]: Texas Instruments Example
[4]: Ercegovac, Milos Lang, Thomas, "Digital Arithmetic"
[5]: Kuo, Lee, Tian, "Real-Time Digital Signal Processing"
log:
01-Jul-2015: Fixed typo in the fixed-point binary word equation.
09-Apr-2013: Updated to use tuple format and use mathjax.
04-Apr-2011: Initial post.
- Comments
- Write a Comment Select to add a comment

One surprise for me when I started using fixed point was that I had to be careful of underflow, not overflow.
With integer math I've become used to making sure I was not performing operations that could lead to numbers becoming too large for the integer space I was using. For instance, multiplying two 16-bit integers needs a 32-bit result to insure that none of the products cause an overflow. With multiple operations it is sometimes necessary to scale down the values to avoid overflow.
With fixed point, my biggest problem has been underflow. Multiplying 0.01 x 0.01 gives a smaller number, 0.0001. I've performed many mathematical operations that ended up with a result of all zeros, due to underflow. I've found that I have to scale up my values to avoid underflow.







it is a very interesting article. i have some fixed point value from a DSP. they are conerted in 16 bit hexa. for exemple:(surprised:x"FFED, 0xFFE7,0x 001A 0x002D ). is there any easy trick to convert them to double value?
for fractional part k starts from 1, i.e (?k=-1FWL?1bF[k]2?k )

Thanks, yes you correct the equation is incorrect. Simply change `k` to start at 1 doesn't completely fix the issue. Need to define how the "fraction" word bits are indexed, there still would be a 0 indexed bit. The equation will be updated ASAP.
nice article...really helpful.
Can somebody please tell how to convert very small value like for eg: 0.000000058323780584287955 to fixed point???
thank you
function [y,L,B] = QCoeff(x,N)
% [y,L,B] = QCoeff(x,N)
% Coefficient Quantization using N=1+L+B bit Representation
% with Rounding operation
% y: quantized array (same dim as x)
% L: number of integer bits
% B: number of fractional bits
% x: a scalar, vector, or matrix
% N: total number of bits
xm = abs(x);
L = max(max(0,fix(log2(xm(:)+eps)+1))); % Integer bits
if (L > N)
errmsg = [ *** N must be at least ,num2str(L), ***]; error(errmsg);
end
B = N-L; % Fractional bits
y = xm./(2^L); y = round(y.*(2^N)); % Rounding to N bits
y = sign(x).*y*(2^(-B)); % L+B+1 bit representation
Hello to all, I want to developing an maximum likelihood algorithm in verilog in this I am unable to define matrix , division , square... Please some on help me to develop this sub block or if you have any suggestions to develop ML algorithm in verilog please help me..

@ravishosamani you might be better off with one of the HLS tools
If you don't have much experience implementing what you described in an event-oriented HDL (e.g. Verilog and VHDL), a C based HSL might be more appropriate in your case.
Hello,
I know that resolution of a signed 2's complement fixed point number that has b digits in the fractional part equals 1/2^b. In fact resolution=1/2^b.
my question is that if b increases what happens to resolution? considering formula the resolution will decrease. but I think resolution will increase because we can have more fractional numbers. Would you guide me please!

1/2^b is the step size between values. A high resolution is a small step size. Increasing b will reduce the step size and therefore increase the resolution
To post reply to a comment, click on the 'reply' button attached to each comment. To post a new comment (not a reply to a comment) check out the 'Write a Comment' tab at the top of the comments.
Please login (on the right) if you already have an account on this platform.
Otherwise, please use this form to register (free) an join one of the largest online community for Electrical/Embedded/DSP/FPGA/ML engineers: